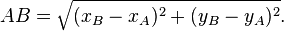

Les fonctions nous servent à modéliser des situations très diverses (pyramide des âges, distance de freinage, évolution de l’offre et la demande...) sous la forme de courbes. En économie elle peuvent représenter des phénomènes continus comme par exemple l’évolution des bénéfices en fonction de la quantité vendue.
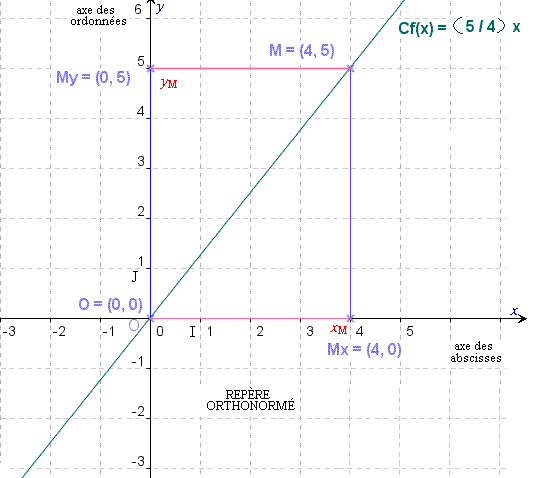
La courbe C a pour équation y = f(x).
L’équation f(x) = 5 a pour inconnue le nombre x, c’est à dire une abscisse. Ici f(x) = 5 pour x = 4.
Est une fonction linéaire, toute fonction numérique à variable réelle f(x) = ax.
Si f est une fonction linéaire, sa courbe est une droite qui passera forcément par 0.
Un nombre qui a une image, a une seule image.
Pour calculer une image, on remplace x par sa valeur.
Si f(5) = 5/4 x alors l’image sera égal à 5/4 * 5/1 = 6,25 ; y = 6,25
Un nombre peut avoir 0 ou plusieurs antécédents.
Pour calculer un antécédent, on résoud l’équation.
Si f(5) = 5/4 x alors l’antécédent sera égal à 5/4 x = 5 ; x = 5/1 / 5/4 ; x = 5/1 * 4/5 ; x = 4
Une fonction est croissante quand elle monte, décroissante quand elle redescend et monotone lorsqu’elle stagne. Le tableau de variation d’une fonction permet de délimiter les intervalles sur lesquelles la fonction varie ainsi que les maximas et minimas.

Une fonction est continue lorsque sa courbe représentative peut être tracée sans lever le crayon.
Si une fonction est dérivable sur I alors elle est continue sur I.
On dit qu'une fonction est convexe sur I lorsque la courbe représentative de la fonction f est entièrement au-dessus de chacune de ses tangentes.
On dit qu'une fonction est concave sur I lorsque la courbe représentative de la fonction f est entièrement au-dessous de chacune de ses tangentes.
Une fonction f est convexe sur I ssi sa dérivée f' est croissante sur I.
Une fonction f est concave sur I ssi sa dérivée f' est décroissante sur I.
La fonction f est convexe sur I ssi sa dérivée seconde f'' est positive sur I.
La fonction f est concave sur I ssi sa dérivée seconde f'' est négative sur I.
Quand la fonction f passe de concave à convexe ou de convexe à concave, elle passe par son point d’inflexion.
On dit que le point A est un point d’inflexion de Cf ssi la dérivée seconde de f s’annule en changeant de signe en l’abscisse du point A.

Soit f une fonction continue sur l'intervale [a ; b]
et k un nombre compris entre f(a) et f(b)
l'équation f(x)=k admet au moins une solution dans [a ; b].
Si en plus d'être continue, f est strictement monotone sur [a ; b]
l'équation f(x)=k admet une unique solution dans [a ; b].

La représentation graphique d’une fonction affine est une droite. Est une fonction affine, toute fonction numérique à variable réelle f(x) = ax + b.
a est le coefficient directeur de la droite et b l’ordonnée à l’origine.
Si a est strictement positif alors la fonction est strictement croissante sur R.
Si a est strictement négatif alors la fonction est strictement décroissante sur R.
Si a = 0 alors la fonction est monotone sur R.
Pour calculer les coordonées de deux points du repère, on donne une valeur à x pour retrouver y. Pour f(x) = 2x + 1
f(0) = 2 * 0 + 1 = 0 + 1 = 1
f(1) = 2 * 1 + 1 = 2 + 1 = 3
La droite passera donc par les points de coordonnées (0 ; 1) et (1 ; 3)
Si A et B sont deux points de coordonnées respectives (xA ; yA) et (xB ; yB), alors le coefficient directeur a = yB - yA / xB - xA
Et l’ordonnée à l’origine b sera égal à : y = ax + b
yA = a*xA + b
-b = a*xA - yA
Deux droites sont parallèles si et seulement si elles ont le même coefficient directeur.
Deux droites sont perpendiculaires si et seulement si le produit de leur coefficient directeur est égal à -1.
1ère étape : Transformons le système en un système équivalent où chaque membre de gauche est y.
D = 2x - 3y = 4
D’ = 4x + y = 1
-3y = -2x + 4
y = -4x + 1
y = 2/3x - 4/3
y = -4x + 1
2ème étape : Trouvons les coordonnées du point d’intersection de D et D’.
D = D’
2/3x - 4/3 = -4x + 1
2/3x + 4/1x = 4/4 + 4/3
2/3x + 12/3x = 12/12 + 16/12
14/3x = 28/12
14/3x = 7/3
x = 7/3 * 3/14
x = 21/42
x = 1/2
y = -4 * ½ + 1
y = -2 + 1
y = -1
Le système proposé a pour solution unique les coordonnées du point commun à D et D’.
Si A et B sont deux points de coordonnées respectives (xA ; yA) et (xB ; yB), alors la distance AB des deux points A et B est donnée par : 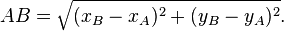
La fonction carrée associe à x son carré f(x) = x².

La représentation graphique de la fonction carrée se nomme parabole dont le sommet est le point O de coordonnées (0 ; 0)
La fonction carré est une fonction paire, sa représentation graphique admet un axe de symétrie qui est l’axe des ordonnées. Elle est décroissante sur l’intervalle ]-oo ; 0] et croissante sur l’intervalle [0 ; +oo[
La fonction carrée est positive ou nulle. Elle admet en 0 un minimum égal à 0; la fonction carrée n’admet pas de maximum.

Pour tous nombres réels positifs a, b, si a < b alors a² < b²
Pour tous nombres réels négatifs a, b, si -a < -b alors a² > b²
La fonction inverse associe à x son inverse f(x) = 1/x.

La représentation graphique de la fonction inverse se nomme une hyperbole.
La fonction inverse est une fonction impaire qui a pour centre de symétrie l’origine 0 du repère. Elle est définie sur l’intervalle ]-oo ; 0[ et sur ]0 ; +oo[, elle est décroissante sur chacun de ces deux intervalles.
La fonction inverse est strictement négative sur l’intervalle ]-oo ; 0[ et strictement positive sur l’intervalle ]0 ; +oo[

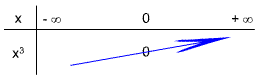
La fonction cube associe à x son cube f(x) = x3
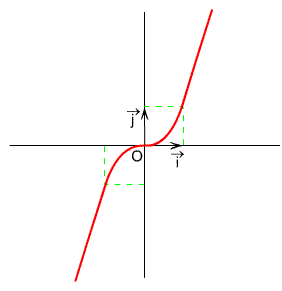
La fonction cube est strictement croissante sur R.
La fonction racine carrée est notée 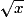
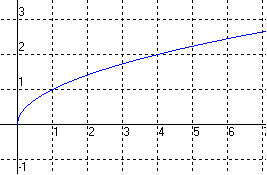
La fonction racine carré est une fonction positive strictement croissante sur l’intervalle [0 ; +oo[. La courbe représentative de cette fonction est une moitié de parabole.

La fonction valeur absolue est notée |x|
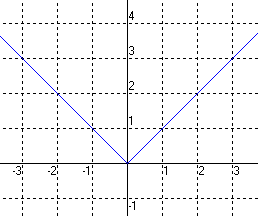
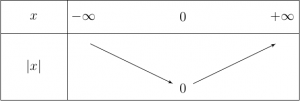
Si x est positif, |x| = x, et si x est négatif, |x| = -x.
La fonction valeur absolue est paire, elle est strictement décroissante sur ]-oo ; 0] et croissante sur [0 ; +oo[

Une fonction homographique est une fonction qui peut être représentée sous la forme d’un quotient de deux fonctions affines. Pour reconnaitre une fonction homographique, il suffit de mettre tous les termes sur le même dénominateur.
La fonction homographique est définie sur R par : f(x) = ax+b / cx+d.
La courbe représentative d’une fonction homographique est une hyperbole qui admet pour asymptote les deux droites d’équation x = -d / c et y = a / c. Le point d’intersection des deux asymptotes est le centre de symétrie pour le graphe.
Si ad - bc < 0 alors l’hyperbole est à l’endroit ; Si ad - bc > 0 alors l’hyperbole est à l’envers.
Les fonctions cosinus et sinus sont périodiques de période 
La courbe du sinus est l’image de la courbe du cosinus par une translation de vecteur 

La fonction cosinus est paire et la fonction sinus est impaire.

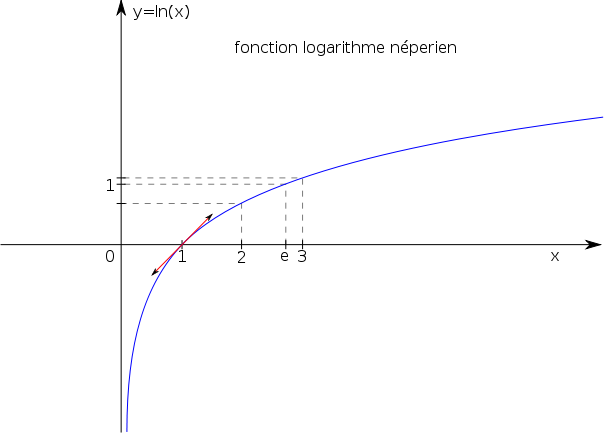

La fonction logarithme népérien, f(x) = ln(x) est strictement croissante sur l’intervalle ]0; +oo[
Si f(x) = ln(x) alors sa dérivée s’écrit : f'(x) = 1/x
Soit pour une fonction composée : (ln u)' = u'/u
La primitive de u'/u est : ln(u) + C
Pour tout réel x > 0 et tout réel y, y = ln(x) Ssi x = ey

ln x = ln y <=> x = y
ln x = y <=> eln x = ey <=> x = ey
ex = ey <=> x = y
ex = y <=> ln ex = ln y <=> x = ln y
Dans un repère orthonormé, les courbes d’équation f(x) = exp(x) et g(x) = ln(x) sont symétriques par rapport à la droite d’équation x = y

La fonction logarithme népérien est la primitive de la fonction inverse, f(x) = 1/x qui s’annule en 1.
ln 1 = 0
L’équation ln x = 1 admet une solution unique dans R cette solution est un irrationnel que l’on note e.
ln e = 1
La fonction logarithme népérien est la réciproque de la fonction exponentielle.
ln(ex) = x
elnx = x
lim ln(x) quand x --> 0 = -oo
lim ln(x) quand x --> +oo = +oo
lim ln(x)/x quand x --> +oo = 0 (croissance comparée)
lim xln(x) quand x --> 0 = 0
lim ln(x+1)/x quand x --> 0 = 1

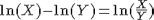
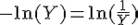

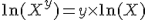


La fonction exponentielle, f(x) = exp(x) est strictement positive, croissante et dérivable sur R.
f(0) = exp (0) = 1
f(1) = exp (1) = e = 2,718
exp(1) = exp(1*x) = exp(1)x = ex
La fonction exponentielle est la seule fonction égale à sa dérivée.
Sa dérivée s’écrit : f'(x) = f(x) = exp(x) = exp'(x) = ex
Soit pour une fonction composée : (eu(x))’ = u’(x) * eu(x)
Sa primitive s’écrit : F(x) = ex
Si f(x) = u'(x) * eu(x) : F(x) = eu(x) + C
La fonction exponentielle est la réciproque de la fonction logarithme népérien.
ln(ex) = x
elnx = x
lim ex quand x --> -oo = 0
lim ex quand x --> +oo = +oo
La fonction exponentielle de base a > 0 s’écrit : ax = ex * ln(a)
La fonction puissance s’écrit : xa = ea * ln(x)
lim ln(x)/xn quand x --> +oo = 0
lim exp(x)/xn quand x --> +oo = +oo (croissance comparée)
La fonction exponentielle croît plus vite que la fonction xn
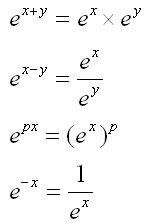

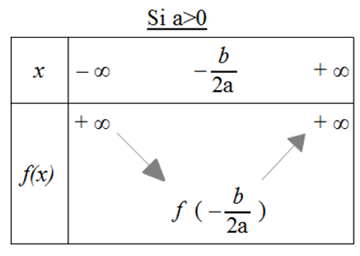
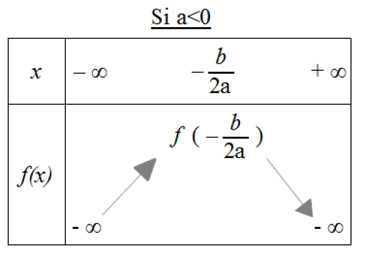
Une fonction polynôme du second degré ou trinôme est une fonction f définie sur R par : f(x) = ax² + bx + c.
La courbe représentative de ce type de fonction est une parabole admettant un axe de symétrie d’équation x = -b / 2a, y = -Delta / 4a et ayant pour sommet S(x;y) = S(-b / 2a ; -Delta / 4a).
Trouver les racines d’un trinôme du second degré, signifie résoudre l’équation ax² + bx + c = 0. Pour cela, il faut d’abord calculer le discriminant Delta.
Delta = b² - 4ac
Toute fonction du second degré possède une forme réduite ou forme canonique f(x) = a ( x - Alpha )² + Beta.
Alpha = -b / 2a
Beta = f(Alpha) = -Delta / 4a
Forme cononique = a ( x + b / 2a )² -Delta / 4a
Ainsi, la fonction f(x)=3(x-1)²-12 peut s’écrire sous 3 formes différentes :
f(x)=3(x-1)²-12 est sa forme canonique
f(x)=3x²-6x-9 est sa forme développée
f(x)=3(x-3)(x+1) est sa forme factorisée
La forme développée sert à vérifier qu’il s’agit bien d’un polynôme du second degré.
La forme factorisée sert à résoudre des équations et inéquations du second degré.
La forme canonique sert à étudier les variations ou trouver un extremum.
Pour avoir un trinôme du second degré sous sa forme canonique, on calcule Alpha et Beta ou on factorise.
Exemple : f(x) = x² - 6x + 5
- on fait apparaître le carré d’une somme, on remarque que x² - 6x + 9 est le développement du carré de (x - 3)²
x² - 6x + 5 = x² - 6x + 9 - 9 + 5
- on met l’expression sous sa forme canonique a ( x - Alpha )² + Beta
(x² - 6x + 9) - 9 + 5 = (x - 3)² - 4
- on factorise à l’aide de l’identité remarquable a² - b² = (a + b)(a - b) pour avoir la forme factorisée
(x - 3)² - 2² = ((x - 3) + 2)) ((x - 3) - 2)) = (x - 1) (x - 5)
Si a différent de 1, on factorise pour se rapprocher de la forme canonique
f(x) = 2x² - 20x + 10 = 2 (x² - 10x) + 10
- on fait apparaître le carré d’une somme, on remarque que x² - 10x + 25 est le développement du carré de (x - 5)²
2 (x² - 10x) + 10 = 2 (x² - 10x + 25 - 25) + 10
- on fait apparaître l’identité remarquable
2 [(x - 5)² - 25] + 10
- on met l’expression sous sa forme canonique a ( x - Alpha )² + Beta
f(x) = 2 (x - 5)² - 40
Pour factoriser un trinôme du second degré, on calcule le discriminant et on applique la formule en fonction de Delta :



Le nombre dérivé en un point d’une fonction est le coefficient directeur de la tangente au graphe de cette fonction en ce point.
Soit f une fonction définie sur l’intervalle I. On appelle fonction dérivée de f la fonction f' qui associe à toute valeur x de I le nombre dérivé f'(x). La fonction dérivée de f(x) est donc notée f'(x) qui représente les variations de la fonction f(x).
Calculer et tracer la fonction dérivée d’une fonction permet donc de visualiser la variation de cette fonction.


Si f est dérivable sur l’intervale I et admet un maximum ou minimum local en un point a, alors f'(a) = 0.
Soit f(x) = 2x² + 4x - 3
f'(x) = 4x + 4 = 0
4x = -4 donc x = -1
f(-1) = 2 - 4x - 3 donc y = -5
Si f est dérivable sur l’intervale I et si f est croissante sur I, alors f' est positive sur I.
Si f est dérivable sur l’intervale I et si f est décroissante sur I, alors f' est négative sur I.