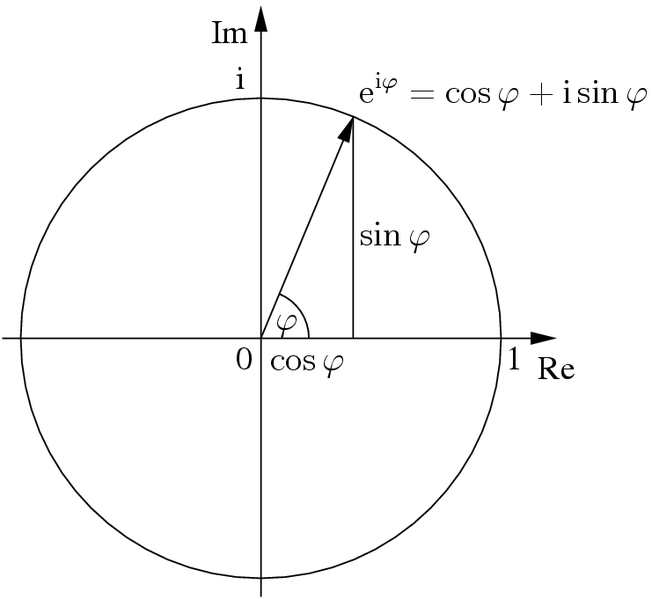
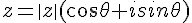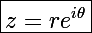Est un nombre complexe tout éléments appartenant à l’ensemble du corps des nombres complexes noté C et s’écrivant z = a + bi (forme algébrique).
On dit que le nombre a est la partie réelle de z que l’on peut noter également Re(z).
On dit que le nombre b est la partie imaginaire de z que l’on peut noter également Im(z).
z = 7 (réel)
z = 3i (imaginaire pur)
z = 3 + 7i (nombre complexe)
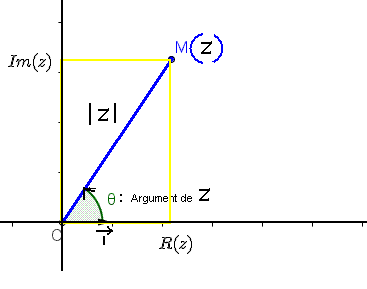
Les règles de calcul sont exactement les mêmes que celles dans R, il faut juste tenir compte que i² = - 1.
Quant on a des fractions avec des complexes au numérateur et au dénominateur, on doit multiplier le numérateur et le dénominateur par la "quantité conjuguée", c’est-à-dire le conjugué du dénominateur.
Pour les équations du second degré, si Delta est négatif, les racines sont alors des complexes et la formule est :

Tout point M (a;b) du plan est l’image d’un nombre complexe z = a + bi.
On dit aussi que z est l’affixe du point M.
Le nombre a - bi est appelé le conjugué de z et se note z barre.
Le module est la distance entre le point M et l’origine du repère.
On appelle module de z la longueur [OM] qu’on note |z|.

Le module est une longueur, il sera donc toujours positif.
L’argument est l’angle entre l’axe des abscisses et la droite (OM).
Un argument de z est une mesure en radians de l’angle 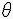
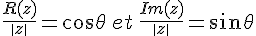
Il faut donc d’abord calculer le module, puis on factorise par le module.