


Un triangle est un polygone à 3 côtés.
La somme des mesures des angles d’un triangle fait 180°.
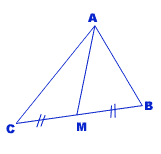
La droite AM est la médiane issue du sommet A. Elle coupe le côté opposé BC à son milieu au point M.
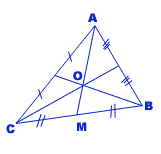
Les trois médianes du triangle se coupent au point O, appelé centre de gravité du triangle.
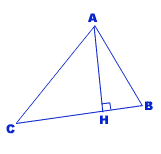
La droite AH est la hauteur issue du sommet A. Elle est perpendiculaire au côté opposé BC.
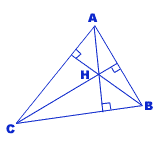
Les trois hauteurs du triangle se coupent au seul point H, appelé orthocentre du triangle.
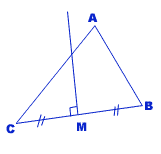
La droite M perpendiculaire à la droite BC et coupant la droite BC en son milieu est une médiatrice.
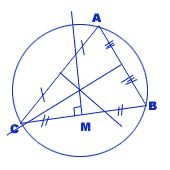
Les 3 médiatrices se coupent en un point qui est le centre du cercle circonscrit au triangle passant par les trois sommets du triangle.
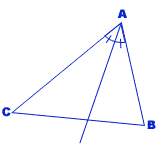
La bissectrice d’un angle est la droite coupant celui-ci en deux angles égaux faisant chacun la moitié de l’angle initial.
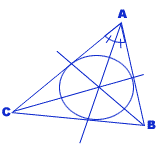
Les 3 bissectrices se coupent en un point qui est le centre du cercle inscrit du triangle tangent aux trois côtés du triangle.
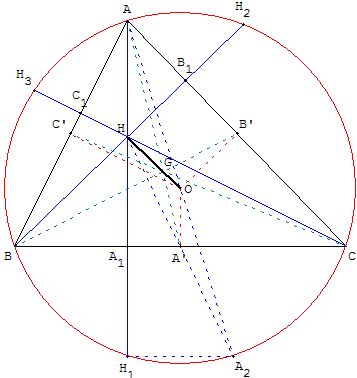
Sur la droite d’Euler les points O, G et H sont alignés et GH = 2 GO (relation d’Euler).
Le théorème de Thalès permet de calculer des rapports de longueur et de mettre en évidence des relations de proportionnalité en présence de parallélisme.
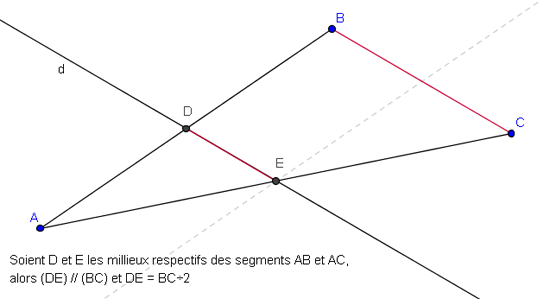
Si deux droites (EC) et (DB) se coupent en A, si les points E, A, C et D, A, B sont alignés dans le même ordre et si les droites (ED) et (BC) sont parallèles alors :
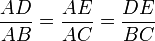
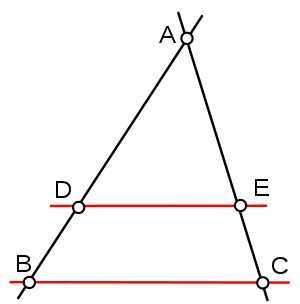
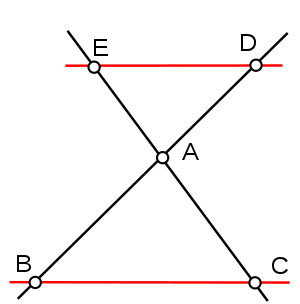
Si dans un triangle, une droite est parallèle à un côté et passe par le milieu d’un autre côté, alors elle passe par le milieu du 3ème côté.
Si dans un triangle, une droite passe par les milieux de deux côtés, alors elle est parallèle au troisième côté.
Dans un triangle, la longueur du segment qui joint les milieux de deux côtés est égale à la moitié de celle du troisième côté.
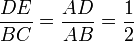
La réciproque du théorème de Thalès permet de savoir si deux droites sont parallèles ou non lorsque l’on connaît des rapports de longueurs.
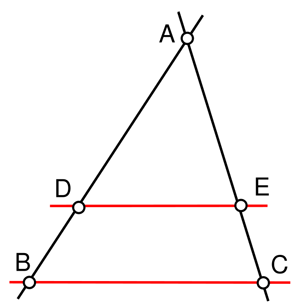
Dans le triangle ABC, les points D et E appartenant respectivement aux segments [AB] et [AC]. Si les points A, D, B et A, E, C sont alignés dans le même ordre et si les rapports AD/AB et AE/AC sont égaux alors les droites (DE) et (BC) sont parallèles.
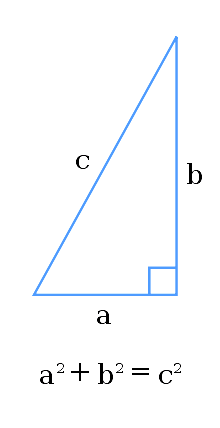
Dans un triangle rectangle le carré de la longueur de l’hypoténuse (le plus long côté) est égal à la somme des carrés des longueurs des deux autres côtés.
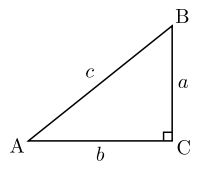
AC² + CB² = AB²
Si, dans un triangle, le carré d’un côté est égal à la somme des carrés des deux autres côtés, alors ce triangle est rectangle.
Si dans un triangle, la médiane issue d’un sommet a une longueur égale à la moitié de la longueur du côté opposé alors le triangle est rectangle en ce sommet.
Dans un triangle rectangle, la médiane issue de l’angle droit est égale à la moitié de la longueur de l’hypoténuse.
Si une corde passe par le centre d’un cercle alors c’est un diamètre.
Un cercle circonscrit à un triangle rectangle à pour centre le milieu de l’hypoténuse de ce dernier.
Si un triangle est rectangle, alors son hypoténuse est un diamètre du cercle circonscrit.
Si un triangle inscrit dans un cercle a un côté pour diamètre, alors il est rectangle et ce côté est l’hypoténuse.