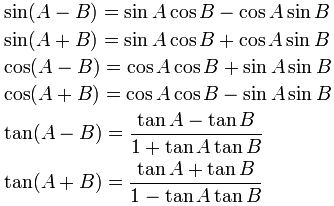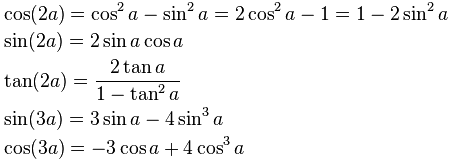La trigonometrie s’emploie à mesurer les angles d’un triangle. À partir d’un triangle, nous utiliserons comme mesure d’angle les degrés. Ce n’est qu’avec le cercle que nous utiliserons les radians.

Si un triangle est rectangle, alors le cosinus de l’un de ses angles aigus est le quotient du côté adjacent à cet angle par l’hypoténuse.

Trouver un cosinus ou un angle aigu avec la calculatrice.
50 cos = 0,64
0,5 cos-1 = 60°
Un sinus ou un cosinus ne peut pas être supérieur à 1.
Comment calculer un angle aigu dans un triangle rectangle connaîssant deux côtés :

Si un triangle est rectangle, alors le sinus de l’un de ses angles aigus est le quotient du côté opposé à cet angle par l’hypoténuse.
Si un triangle est rectangle, alors sa tangente est égale au quotient du côté opposé par le côté adjacent.
Si a est un angle aigu d’un triangle rectangle : tan a = sin a / cos a
Si a est un angle aigu d’un triangle rectangle : (cos a)² + (sin a)² = 1
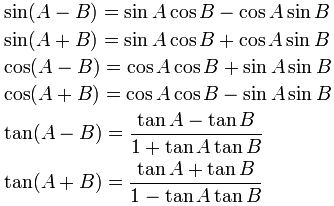
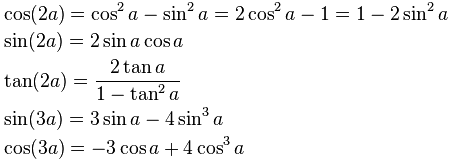
Un cercle trigonométrique est un cercle de rayon 1 sur lequel le sens de déplacement est le sens direct.
cos sur l’axe des abscisses, sin sur l’axe des ordonnées , 0 , Pi/2 , Pi , 3Pi/2, 2Pi.
Pour les Pi/3, on trace le rectangle qui passe par 1/2 et - 1/2 sur l’axe des abscisses.
Pour les Pi/6, on trace le rectangle qui passe par 1/2 et - 1/2 sur l’axe des ordonnées.
Pour les Pi/4, on trace les diagonales.


Le cercle C de centre O et de rayon 1, muni d’une origine I et d’un sens de parcours positif est appelé cercle trigonométrique.
Pour des valeurs en dehors de ]-Pi ; +Pi], la droite s’enroule autour du cercle sur plusieurs tours. Un tour correspond à 2Pi.
On peut symboliser un angle orienté de vecteurs de deux manières :

Parmi toutes les mesures d’un angle orienté (u,v), une seule mesure appartient à l’intervale ]-Pi ; +Pi]. Cette mesure est appellée mesure principale de l’angle.